…what it reveals is interesting, what it conceals is vital.
For decades, physician scientists have been slaves to a p value of 0.05 or less (there is a less than 5% chance that the findings of the study happened due to chance) or if the confidence interval includes zero.


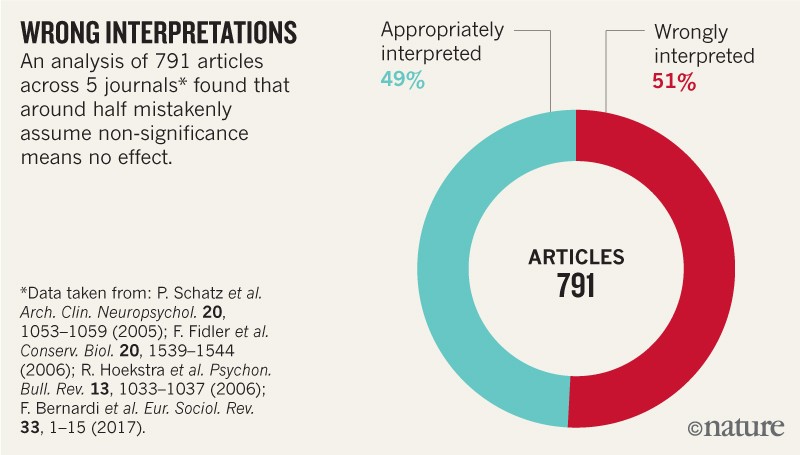
An article in Nature argues that this concept is outdated.
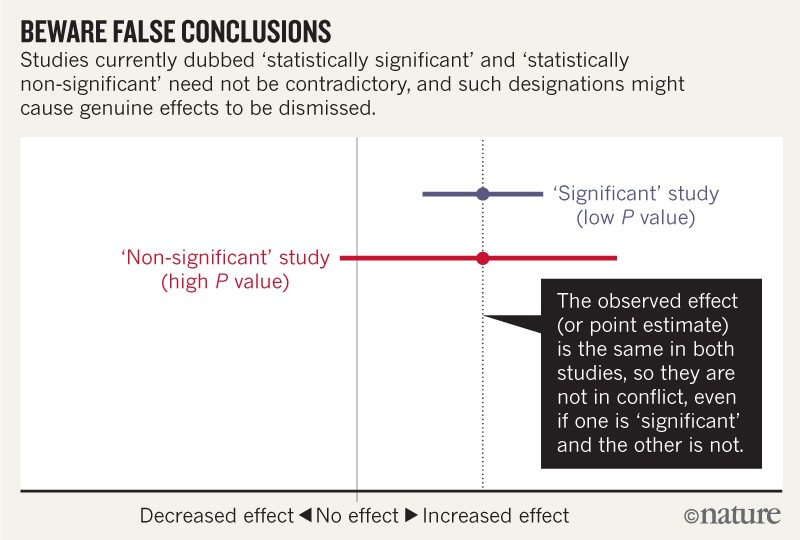
Not statistically significant does not mean no effect.
“Again, we are not advocating a ban on P values, confidence intervals or other statistical measures — only that we should not treat them categorically. One reason to avoid such ‘dichotomania’ is that all statistics, including P values and confidence intervals, naturally vary from study to study, and often do so to a surprising degree.
We must learn to embrace uncertainty. One practical way to do so is to rename confidence intervals as ‘compatibility intervals’ and interpret them in a way that avoids overconfidence.When talking about compatibility intervals, bear in mind four things:
1. Just because the interval gives the values most compatible with the data, given the assumptions, it doesn’t mean values outside it are incompatible; they are just less compatible. In fact, values just outside the interval do not differ substantively from those just inside the interval. It is thus wrong to claim that an interval shows all possible values.
2. Not all values inside are equally compatible with the data, given the assumptions. The point estimate is the most compatible, and values near it are more compatible than those near the limits. Interpreting the point estimate, while acknowledging its uncertainty, will keep you from making false declarations of ‘no difference’, and from making overconfident claims.
3. Like the 0.05 threshold from which it came, the default 95% used to compute intervals is itself an arbitrary convention. It is based on the false idea that there is a 95% chance that the computed interval itself contains the true value, coupled with the vague feeling that this is a basis for a confident decision.4. Be humble: compatibility assessments hinge on the correctness of the statistical assumptions used to compute the interval. In practice, these assumptions are at best subject to considerable uncertainty. Make these assumptions as clear as possible and test the ones you can, for example by plotting your data and by fitting alternative models, and then reporting all results.
I’ll leave you with some thoughts about statistics:








